रेखाएँ और कोण
रेखाएँ और कोण ज्यामिति में प्रयुक्त मूल शब्द हैं। वे ज्यामिति की सभी अवधारणाओं को समझने के लिए एक आधार प्रदान करते हैं। हम एक रेखा को 1-डी आकृति के रूप में परिभाषित करते हैं जिसे विपरीत दिशाओं में अनंत तक बढ़ाया जा सकता है, जबकि कोण को दो या दो से अधिक रेखाओं को जोड़कर बनाए गए उद्घाटन के रूप में परिभाषित किया जाता है। समस्या की अवधारणा के आधार पर किसी कोण को डिग्री या रेडियन में मापा जाता है।
सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं और उनकी समझ होने से हमें ज्यामिति की दुनिया को बेहतर ढंग से समझने में मदद मिलती है। इस लेख में हम रेखाओं, कोणों, उनके प्रकार, गुणों और अन्य के बारे में विस्तार से जानेंगे।
रेखाओं और कोणों की परिभाषा
रेखाएँ और कोण ज्यामिति का आधार आकार हैं और इनका ज्ञान हमें ज्यामिति की अवधारणा को बेहतर ढंग से समझने में मदद करता है। रेखाओं और कोणों की मूल परिभाषा यह है कि रेखाएँ 1-डी आकृतियाँ हैं जिन्हें विपरीत दिशा में अनंत रूप से बढ़ाया जा सकता है, जबकि कोण को दो रेखाओं के प्रतिच्छेद करने पर मुंह के खुले होने की डिग्री के रूप में परिभाषित किया जाता है। यदि दो प्रतिच्छेदी रेखाओं के बीच चौड़ा स्थान अधिक हो तो उनके बीच का कोण अधिक होता है।
इन अवधारणाओं का उपयोग विभिन्न शब्दों को परिभाषित करने के लिए अत्यधिक किया जाता है और ये छात्रों के लिए ज्यामिति का अध्ययन करने में बहुत सहायक होते हैं। आइए अब इनके बारे में विस्तार से जानें।
रेखाएँ क्या हैं?
रेखा को एक आयामी आकृति के रूप में परिभाषित किया गया है जिसे अनंत तक बढ़ाया जा सकता है। इसका विस्तार दोनों दिशाओं में हो सकता है और एक रेखा की लंबाई अनंत होती है। हम एक रेखा को उन अनंत बिंदुओं के संग्रह के रूप में भी परिभाषित कर सकते हैं जो एक साथ जुड़कर एक सतत आकृति बनाते हैं।
एक रेखा का कोई प्रारंभिक बिंदु या समापन बिंदु नहीं होता है। यदि किसी रेखा का एक प्रारंभिक बिंदु और एक अंतिम बिंदु है तो उसे रेखाखंड कहा जाता है, जबकि यदि किसी रेखा का केवल एक प्रारंभिक बिंदु है लेकिन कोई अंत बिंदु नहीं है तो उसे किरण कहा जाता है।
रेखाओं और कोणों के प्रकार
इस विषय में हम ज्यामिति में वर्गीकृत सभी विभिन्न प्रकार की रेखाओं और कोणों के बारे में जानेंगे।
रेखाओं के प्रकार
हम रेखाओं को उनके समापन बिंदु और प्रारंभिक बिंदु के आधार पर वर्गीकृत कर सकते हैं,
- रेखा खंड
- किरण
रेखाओं को इस प्रकार भी वर्गीकृत किया जा सकता है,
- समानांतर रेखाएं
- लम्बवत रेखायें
- अनुप्रस्थ रेखाएँ
आइए अब इनके बारे में विस्तार से जानें।
रेखा खंड
रेखाखंड एक रेखा का वह भाग है जिसके दो अंतबिंदु होते हैं। यह दो बिंदुओं के बीच की सबसे छोटी दूरी है और इसकी एक निश्चित लंबाई होती है और इसे आगे नहीं बढ़ाया जा सकता है। नीचे जोड़ी गई छवि में एक रेखाखंड AB दिखाया गया है:

किरण
किरण वह रेखा है जिसका एक आरंभिक बिंदु या अंतिम बिंदु होता है और जो एक दिशा में अनंत की ओर बढ़ती है। नीचे जोड़ी गई छवि में एक किरण OA दिखाया गया है। यहां O प्रारंभिक बिंदु है और A की ओर बढ़ रहा है।

लम्बवत रेखायें
जब दो रेखाएं एक-दूसरे से समकोण बनाती हैं और एक ही बिंदु पर मिलती हैं तो उन्हें लंबवत रेखाएं कहा जाता है। नीचे जोड़ी गई छवि में दो लंबवत रेखाएँ AB और CD दिखाई गई हैं:

समानांतर रेखाएं
समानांतर रेखाएँ वे रेखाएँ होती हैं जो किसी भी बिंदु पर एक समतल पर एक दूसरे से नहीं मिलती हैं और एक दूसरे को नहीं काटती हैं। समांतर रेखाओं के किन्हीं दो बिंदुओं के बीच की दूरी निश्चित होती है। नीचे जोड़ी गई छवि में दो समानांतर रेखाएँ l और m दिखाई गई हैं:

अनुप्रस्थ रेखाएँ
जब दो दी गई रेखाएं एक दूसरे को एक अलग बिंदु पर काटती हैं, तो उन्हें अनुप्रस्थ रेखाएं कहा जाएगा। रेखा n , रेखा l और रेखा m की अनुप्रस्थ रेखा है जैसा कि नीचे जोड़ी गई छवि में दिखाया गया है:

अनुप्रस्थ रेखाएँ और कोण
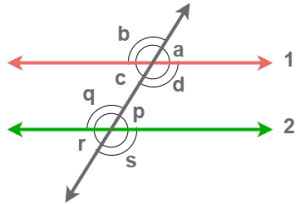
समानांतर रेखाओं और अनुप्रस्थ रेखाओं के प्रतिच्छेदन से बनने वाले विभिन्न कोण हैं,
- संगतकोण
- एकांतर अंतः कोण
- एकांतर बाह्य कोण
- लंबवत् विपरीत कोण
आइए इसके बारे में विस्तार से जानें।
संगतकोण
कोणों के निम्नलिखित जोड़े जो ऊपर जोड़े गए चित्र से संगतकोण कोण हैं, हैं:
- ∠a = ∠p
- ∠b = ∠q
- ∠d = ∠s
- ∠c = ∠r
एकांतर बाह्य कोण
कोणों के निम्नलिखित जोड़े जो ऊपर जोड़े गए चित्र से एकांतर बाह्य कोण हैं, हैं:
- ∠a = ∠r
- ∠b = ∠s
एकांतर अंतः कोण
ऊपर जोड़े गए चित्र से कोणों के निम्नलिखित जोड़े एकांतर आंतरिक कोण हैं,
- ∠d = ∠q
- ∠c = ∠p
लंबवत् विपरीत कोण
कोणों के निम्नलिखित जोड़े जो ऊपर जोड़े गए चित्र से लंबवत् विपरीत कोण हैं, हैं:
- ∠a = ∠c
- ∠बी = ∠डी
- ∠p = ∠r
- ∠q = ∠s
नीचे जोड़ी गई तालिका सभी प्रकार के कोणों को दर्शाती है जो समानांतर रेखाओं और एक तिर्यक रेखा की जोड़ी से बनते हैं।
| कोणों का युग्म बना | कोणों के बीच संबंध |
|---|---|
| संगतकोण | ∠a = ∠p ∠b = ∠q ∠d = ∠s ∠c = ∠r |
| एकांतर अंतः कोण | ∠a = ∠r ∠b = ∠s |
| एकांतर बाह्य कोण | ∠d = ∠q ∠c = ∠p |
| लंबवत् विपरीत कोण | ∠a = ∠c ∠बी = ∠डी ∠p = ∠r ∠q = ∠s |
रेखाओं के गुण
रेखाओं के विभिन्न गुण हैं,
- यदि तीन या तीन से अधिक बिंदु एक ही रेखा में स्थित हों तो उन्हें संरेख बिंदु कहा जाता है।
- दो रेखाएँ समानान्तर रेखाएँ कहलाती हैं यदि उनके बीच की दूरी सदैव स्थिर रहती है।
- यदि रेखाएँ समकोण पर प्रतिच्छेद करती हैं तो वे लम्ब रेखाएँ कहलाती हैं।
कोण क्या हैं?
जब दो किरणों के अंतिम बिंदु एक उभयनिष्ठ बिंदु पर मिलते हैं तो इस प्रकार बनी आकृति को कोण कहा जाता है। एक कोण को या तो डिग्री या रेडियन में मापा जाता है और हम आसानी से डिग्री को रेडियन में बदल सकते हैं। हम किसी कोण को दर्शाने के लिए ‘∠’ का उपयोग करते हैं।
माप के आधार पर कोण विभिन्न प्रकार के होते हैं। उनकी चर्चा नीचे की गई है,
कोणों के प्रकार
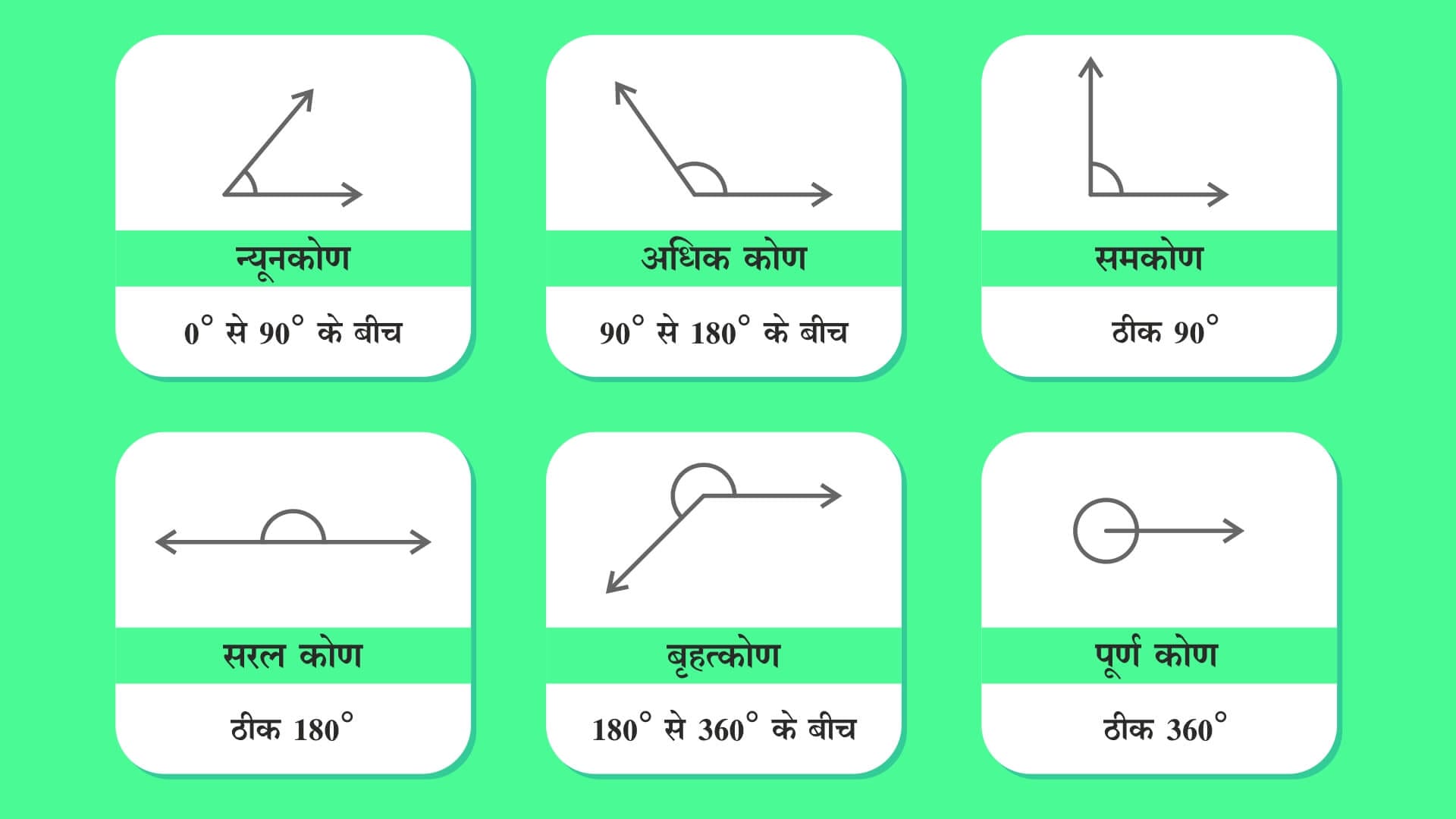
माप और विभिन्न परिदृश्यों के आधार पर ज्यामिति में विभिन्न प्रकार की रेखाएँ और कोण होते हैं। आइए हम यहां उन सभी रेखाओं और कोणों को उनकी परिभाषाओं के साथ जानें।
- न्यूनकोण
- अधिक कोण
- समकोण
- सरल कोण या ऋजु कोण
- बृहत्कोण
- पूर्ण कोण
न्यूनकोण
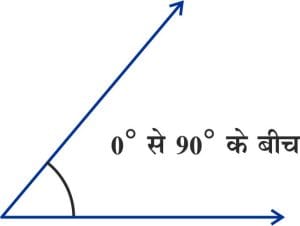
जब कोण समकोण से छोटा होता है तो वह न्यूनकोण कहलाता है। इसका माप इसका माप 0 डिग्री से 90 डिग्री के बीच होता है होता है। नीचे जोड़ी गई छवि एक न्यून कोण दिखाती है:
अधिक कोण
जब कोण की माप समकोण से अधिक हो तो उसे अधिक कोण कहते हैं।इसका माप 90 डिग्री से 180 डिग्री के बीच होता है। नीचे जोड़ी गई छवि एक अधिक कोण दिखाती है:

समकोण
जब कोण का माप ठीक 90 डिग्री होता है तो उसे समकोण कहते हैं। नीचे जोड़ी गई छवि एक समकोण दिखाती है:

सरल कोण (ऋजु कोण)
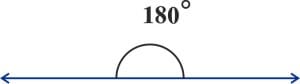
यदि किसी कोण की माप 180 डिग्री है तो इस प्रकार बने कोण को सरल कोण कहा जाता है। नीचे जोड़ी गई छवि एक सीधा कोण दिखाती है।
बृहत्कोण
जब कोण की माप 180° से अधिक तथा 360° से कम हो तो इसे बृहत्कोण कोण कहते हैं। नीचे जोड़ी गई छवि रिफ्लेक्स एंगल दिखाती है

पूर्ण कोण
जब कोण की माप 360° हो तो उसे पूर्ण कोण कहते हैं। नीचे जोड़ी गई छवि पूर्ण कोण दिखाती है।

हम कोणों को इस प्रकार भी वर्गीकृत कर सकते हैं,
- पूरक कोण
- संपूरक कोण
- आसन्न कोण
- लंबवत् विपरीत कोण
पूरक कोण
जब दो कोणों का योग 90° होता है, तो उन्हें पूरक कोण कहा जाता है। नीचे दी गई छवि में दो पूरक कोण AOB और BOC दिखाए गए हैं।

संपूरक कोण
जब दो कोणों का योग 180° हो तो वे संपूरक कोण कहलाते हैं। नीचे दी गई छवि में दो पूरक कोण PMN और QMN दिखाए गए हैं।

आसन्न कोण
जब दो कोणों में एक उभयनिष्ठ भुजा और एक उभयनिष्ठ शीर्ष होता है और शेष दो भुजाएं उभयनिष्ठ भुजा की एकांतर भुजाओं पर स्थित होती हैं तो उन्हें आसन्न कोण कहा जाता है। नीचे दी गई छवि में दो आसन्न कोण A और B दिखाए गए हैं।

लंबवत् विपरीत कोण
जब दो कोण एक-दूसरे के विपरीत हों और दो रेखाएँ एक-दूसरे को एक उभयनिष्ठ बिंदु पर काटती हों, तो उन्हें लंबवत् विपरीत कोण कहा जाता है। नीचे जोड़ी गई छवि में दो कोण AOB और COD दिखाए गए हैं।
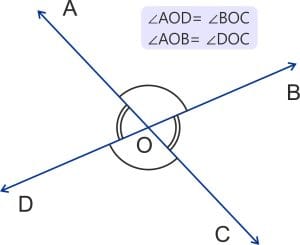
- ∠AOD= ∠BOC
- ∠AOB= ∠DOC
त्रिभुज में कोणों का योग 180° तक होता है
किसी भी त्रिभुज के सभी कोणों का योग 180° होता है। यह नीचे सिद्ध है, मान लीजिए हमारे पास एक त्रिभुज ABC है जैसा कि नीचे दी गई छवि में दिखाया गया है:

- ∠A + ∠B + ∠C = 180°
रेखाओं और कोणों के गुण
इस अनुभाग में, हम रेखाओं और कोणों के कुछ सामान्य गुणों के बारे में जानेंगे
रेखाओं के गुण
रेखा के निम्नलिखित गुण हैं
- रेखा का केवल एक ही आयाम अर्थात् लंबाई होती है।इसमें चौड़ाई और ऊंचाई नहीं है.
- एक रेखा पर अनंत बिंदु होते हैं।
- एक रेखा पर स्थित तीन बिंदुओं को संरेख बिंदु कहा जाता है
कोणों के गुण
कोणों के निम्नलिखित गुण हैं
- कोण बताते हैं कि कोई व्यक्ति अपनी स्थिति से कितना घूम चुका है।
- जब दो रेखाएँ मिलती हैं तो कोण बनते हैं और उन्हें कोण की भुजाएँ कहा जाता है।
रेखाओं और कोणों पर उदाहरण-
उदाहरण 1: यदि ∠x का मान 65 डिग्री है, तो ∠x का प्रतिवर्ती कोण ज्ञात करें।
(A) 295
(B) 285
(C) 175
(D) 25
समाधान: (A)
अब, रेखाओं और कोणों के गुणों के अनुसार, एक कोण और उसके प्रतिवर्ती कोण का योग 360° होता है।
इस प्रकार,
∠x + ∠y = 360°
75° + ∠y = 360°
∠y = 360° − 65°
∠y = 295°
इस प्रकार, 65° का प्रतिवर्ती कोण 295° है।
उदाहरण 2: यदि ∠x का मान 75 डिग्री है, तो ∠x का पूरक कोण ज्ञात करें।
(A) 25
(B) 15
(C) 45
(D) 30
समाधान: (B)
अब, रेखाओं और कोणों के गुणों के अनुसार, एक कोण और उसके पूरक कोण का योग 90° होता है।
इस प्रकार,
∠x + ∠y = 90°
75° + ∠y = 90°
∠y = 90° − 75°
∠y = 15°
इस प्रकार, 75° का पूरक कोण 15° है।
उदाहरण 3: यदि ∠x का मान 45 डिग्री है, तो ∠x का संपूरक कोण कोण ज्ञात करें।
(A) 215
(B) 145
(C) 45
(D) 135
समाधान: (D)
अब, रेखाओं और कोणों के गुणों के अनुसार, एक कोण और उसके संपूरक कोण का योग 180° होता है।
इस प्रकार,
∠x + ∠y = 180°
75° + ∠y = 180°
∠y = 180° − 45°
∠y = 135°
इस प्रकार, 75° का संपूरक कोण 135° है।